Lektion F08: Symmetrie bei Funktionen

Was ist Symmetrie?

Wie funktionieren Achsensymmetrie und Punktsymmetrie?

Wie erkennt man Symmetrie am Graphen und wie kann man sie rechnerisch nachweisen?

Wie erkennt man bereits an der Funktionsgleichung die Symmetrieart?

Was sind gerade und ungerade Funktionen?

Wie entstehen die Formeln für die Symmetrie zu einer beliebigen Senkrechten und zu einem beliebigen Punkt?

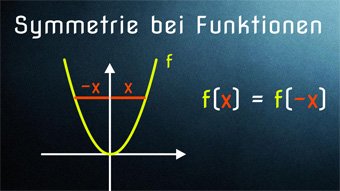
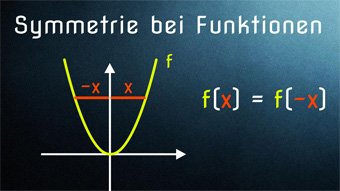
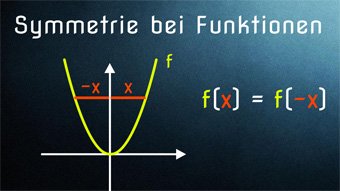
Wir schauen uns die Symmetrie zur y-Achse f(x)=f(-x) und die Symmetrie zum Koordinatenursprung f(x)=-f(-x) an. Wir zeigen, wie man auf die Formeln kommt und wie man die Symmetrie am Graphen erkennt.

 

Wie kann man rechnerisch nachweisen, ob eine Funktion symmetrisch ist und welche Symmetrie vorliegt. Wie erkennt man bereits an der Funktionsgleichung die Symmetrieart (anhand der Exponenten). Begriffe: Gerade Funktion und ungerade Funktion. Koeffizienten beeinflussen Symmetrie nicht.

 

Ermittlung der Formeln für die Symmetrie zu einer beliebigen Senkrechten f(a+x)=f(a-x) und zu einem beliebigen Punkt (Symmetriezentrum) mit f(a+x)-b = -f(a-x)+b. Übungsaufgaben zur Symmetrie. Symmetrie bei linearen Graphen, konstanter Funktion, Asymptote, Sinus- und Kosinusgraphen.

Hierzu gibt es keine Rechner.