Lektion VEK04: Vektorsubtraktion

Was ist der Gegenvektor?

Wie subtrahiert man Ortsvektor mit Verschiebungsvektor?

Wie subtrahiert man mehrere Vektoren?

Wie berechnet man den Umfang eines Dreiecks mit Hilfe der Subtraktion von Vektoren?

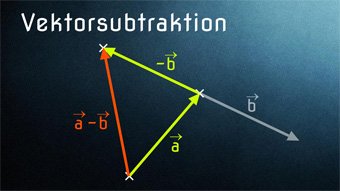
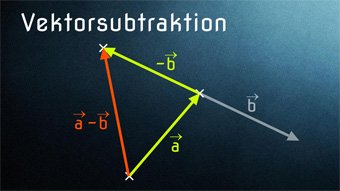
Nachdem wir die Vektoraddition kennengelernt haben, folgt nun ihre „Umkehrung“, die Vektorsubtraktion. Hierzu nutzen wir den sogenannten Gegenvektor.

Für die Dreiecksaufgabe in Teil 2 ist es notwendig, dass ihr wisst, wie man die Vektorlänge berechnet.

 

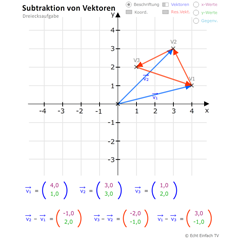
Vektorsubtraktion mit dem Gegenvektor. Vektor a - Vektor b als Vektor a + Gegenvektor b. Geometrische Deutung der Subtraktion bei Ortsvektoren. Reihenfolge der Subtraktion entscheidet über die Richtung des resultierenden Vektors. Subtraktion von Verschiebungsvektoren.

 

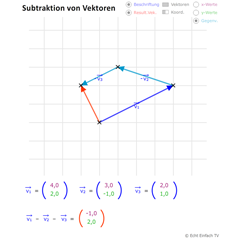
Die gegebenen Dreieckspunkte werden als Ortsvektoren interpretiert, danach subtrahieren wir die Ortsvektoren, um die Vektoren zwischen ihnen zu erschaffen. Anschließend erhalten wir mittels der Vektorlängen den Dreiecksumfang. Rechnerisch und geometrische Darstellung.

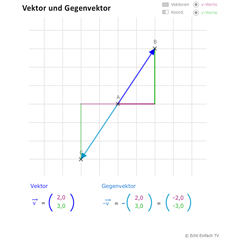
Wird ein Vektor gedreht, sodass er in die entgegengesetzte Richtung zeigt, nennen wir ihn Gegenvektor. Seine Komponenten sind im Vorzeichen getauscht. Er hat jedoch die gleiche Länge.

 

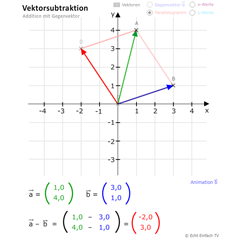
Dieses Programm stellt die Vektorsubtraktion geometrisch dar, mit Verschiebung des Vektors b als Gegenvektor auf den Vektor a.

 

Drei Punkte sind gegeben, die wir zu Ortsvektoren wandeln können. Subtrahieren wir die Ortsvektoren, so erhalten wir die Vektoren zwischen ihnen.

 

Mit diesem Programm können Vektoren auf der Ebene beliebig verschoben werden. Beim korrekten Anordnen der Vektoren als Gegenvektoren ergibt sich der resultierende Vektor.